Finding the Equation of a Line Given Two Points Worksheet

Article: Finding the Equation of a Line Given Two Points Worksheet

When it comes to algebra, one of the fundamental concepts is finding the equation of a line given two points. This skill is essential in various fields such as physics, engineering, and economics. By understanding how to determine the equation of a line, you can analyze and predict patterns and relationships in data sets accurately.

In mathematics, a line is defined by two points, and the equation of a line describes the relationship between its x and y coordinates. By finding the equation of a line given two points, you can determine the slope and y-intercept, which are crucial in graphing and solving linear equations.

Finding the Equation of a Line Given Two Points Worksheet

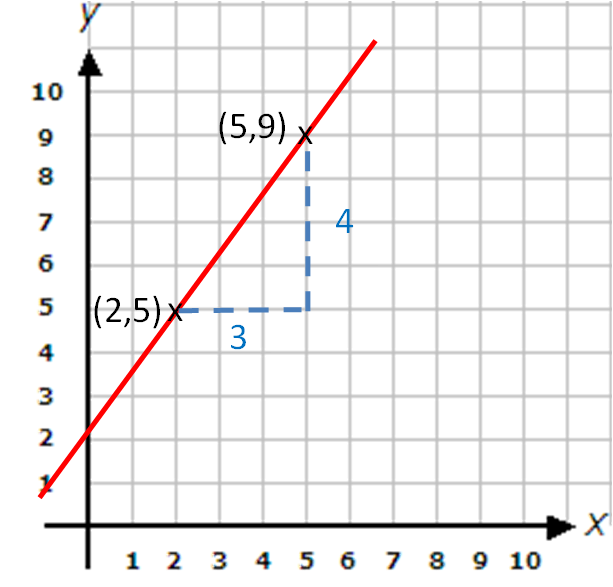
To find the equation of a line given two points, you need to calculate the slope first. The slope (m) of a line passing through two points (x1, y1) and (x2, y2) can be found using the formula: m = (y2 – y1) / (x2 – x1). Once you have the slope, you can determine the y-intercept (b) using the equation: y = mx + b, where b = y – mx.

For example, suppose you have two points (3, 5) and (7, 9). To find the equation of the line passing through these points, you would first calculate the slope: m = (9 – 5) / (7 – 3) = 1. Next, you can substitute the slope into the equation y = mx + b and use one of the points to solve for the y-intercept. In this case, the equation of the line would be y = x + 2.

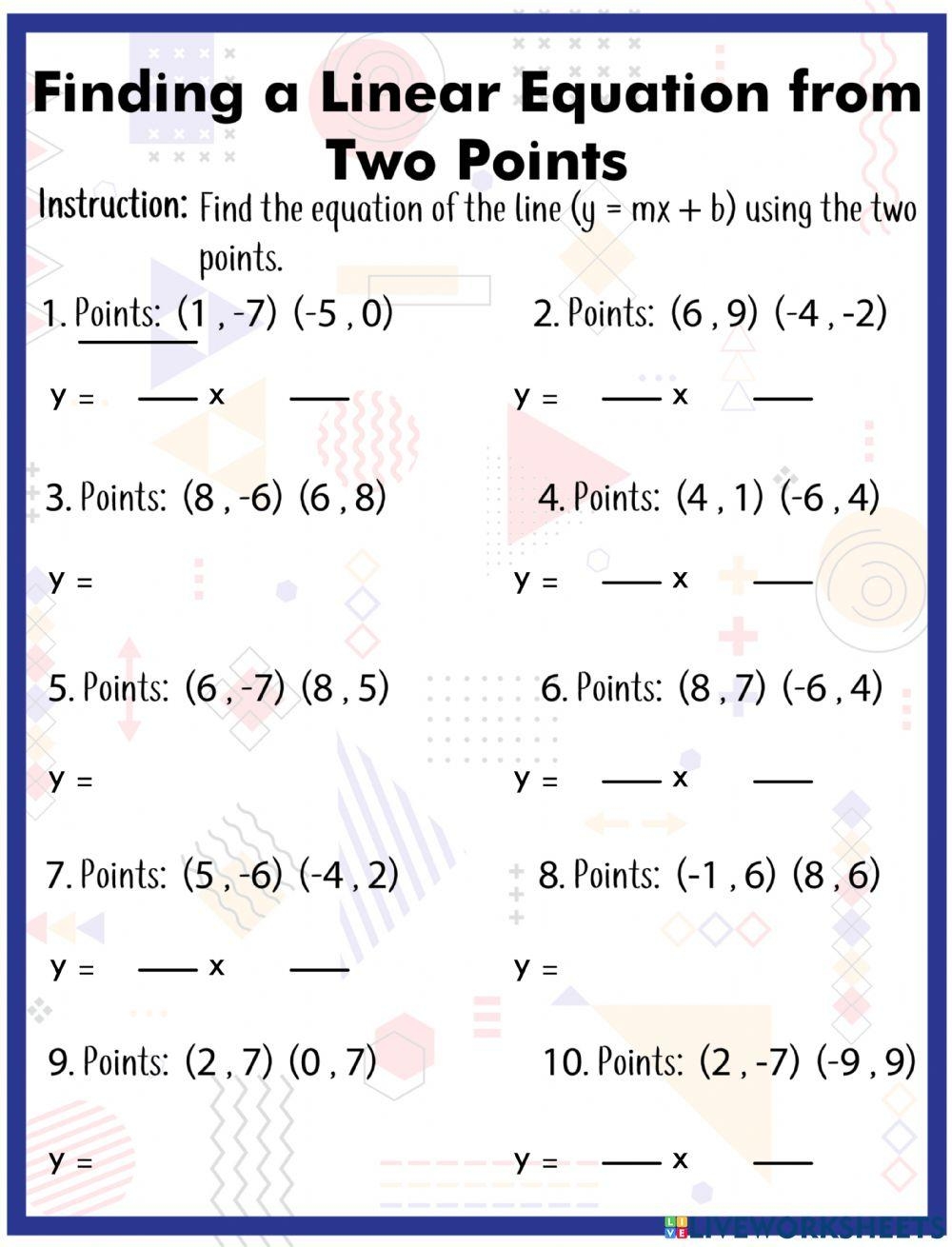
By practicing with worksheets that provide various sets of points, you can enhance your understanding of finding the equation of a line given two points. These worksheets typically include exercises where you have to calculate the slope, determine the y-intercept, and write the equation of the line. Through repetition and practice, you can master this essential algebraic skill.

In conclusion, finding the equation of a line given two points is a crucial skill in algebra that has practical applications in various fields. By understanding how to calculate the slope and y-intercept, you can accurately describe the relationship between two points on a line. Utilizing worksheets and practice exercises can help reinforce this concept and improve your problem-solving abilities in algebraic equations.