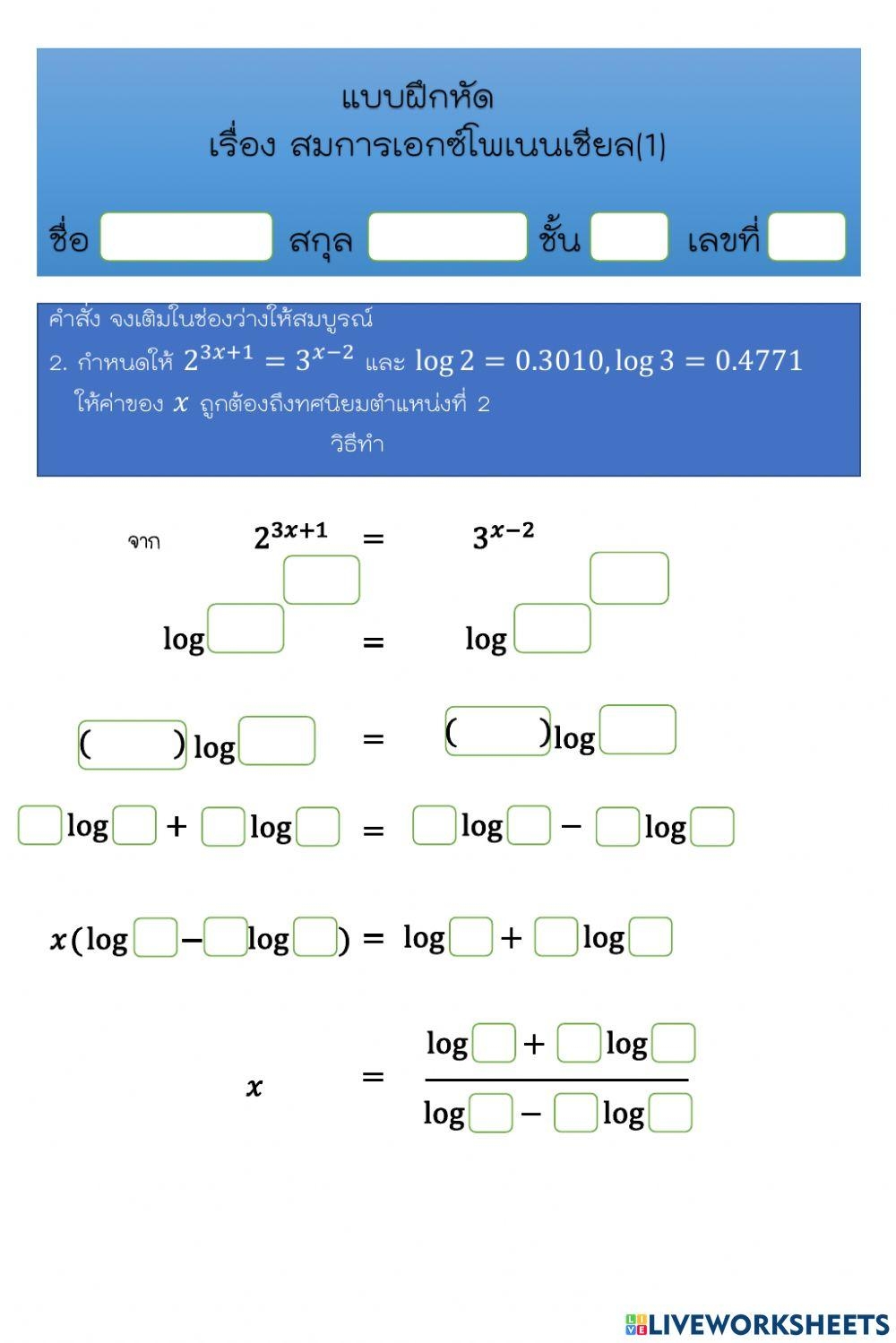
Exponential equations can sometimes be tricky to solve, especially when the variable is in the exponent. However, with the help of logarithms, these equations can be simplified and solved more easily. Logarithms are the inverse operations of exponential functions, so they can be used to “undo” the exponentiation in an equation.
When faced with an exponential equation, one approach is to take the logarithm of both sides of the equation. This allows us to bring the exponent down and solve for the variable. Logarithms can be used to solve equations involving exponential functions because they can convert the equation into a more manageable form.
For example, consider the equation 2^x = 16. By taking the logarithm of both sides, we can rewrite the equation as log(2^x) = log(16). Using the property of logarithms that allows us to bring the exponent down, we get x * log(2) = log(16). Solving for x, we find that x = log(16) / log(2).
Logarithms can also be used to solve exponential equations with variables in both the base and the exponent. By taking the logarithm of both sides and using properties of logarithms, these equations can be simplified and solved step by step. Keeping track of the rules of logarithms is key to successfully solving these types of equations.
When practicing solving exponential equations using logarithms, worksheets can be a helpful tool. These worksheets provide a variety of equations to work through, allowing students to practice applying logarithms to different types of exponential equations. By working through these problems, students can improve their understanding of how logarithms can be used to solve exponential equations.
Overall, solving exponential equations using logarithms can be a useful technique for simplifying and solving equations involving exponents. By understanding the properties of logarithms and practicing with worksheets, students can become more comfortable with this method of solving equations. With practice and patience, solving exponential equations using logarithms can become a valuable skill in algebra and beyond.